Jeg blir alltid positivt overrasket når det etter mangfoldige år etter endt studie plutselig blir behov for et konsept man lærte på skolebenken, og som man den gang ikke kunne se for seg kom til å være nyttig!
I dag var dette konseptet Kumulativ binomisk sannsynlighet.
På vegne av de pårørte i saken må jeg sensurere hva problemstillingen egentlig bestod av, men jeg skal prøve å få gjennom budskapet med hjelp av et like så realistisk og heidundrende spennende eksempel!
Forord
Vi ser for oss en bedrift som selger album av katter, og gir bort album som ikke inneholder katter gratis(hvem bryr seg vel om disse?).
Du og ditt team i bedriften har laget den optimale, ultimate maskinlæremodellen for gjenkjenning av katter i bilder. Dere har laget en modell med en nøyaktighet på hele 98%!
Ledelsen setter kurs
Utifra disse fantastiske resultatene bestemte ledelsen seg for at fra og med nå skal album genereres automatisk!
Albumene kan ha vilkårlig lengde men ikke færre enn 5.
Bildene blir funnet ved å browse millioner av uklassifiserte bilder og selektert ved bruk av vår super-AI.
Problemstilling
Det er svært viktig for ledelsen at kunder som kjøper at kattealbum faktisk får et album med katter. Da retur av album og klager fra misfornøyde kunder er ekstremt viktig å unngå.
Det er også viktig å redusere antallet faktiske kattealbum som gis bort gratis med en feiltakelse.
Ledelsen ønsker å få tall fra teamet på hva sannsynligheten for at disse problemene kan inntreffe er.
For å besvare dette spørsmålet definerer vi først følgende:
Vi har 4 forskjellige album som kan bli generert:
-
Ekte Kattealbum
Et album der flertallet av bildene er av katter, og som blir solgt som et kattealbum. -
Ekte Gratis album
Et album uten kattebilder, disse blir gitt bort gratis. (verdiløst i følge ledelsen). -
Falsk Kattealbum
Et album som ikke inneholder katter, men som blir feilaktig solgt som et kattealbum! -
Falsk Gratisalbum
Et album som inneholder flertall katter, men som blir feilaktig gitt bort gratis.
Løsningen
Før vi avslører den “snasne” løsningen skal vi ta en liten trip down memory lane. Rettere sagt min unødvendig slitsomme vei til Rome.
Vi starter det hele med et eksempel:
Hva er sannsynligheten for at et påstått album med 5 bilder faktisk inneholder 5 bilder av katter?
For å beregne dette multipliserer vi sannsynligheten for å detektere en katt med seg selv 5 ganger.
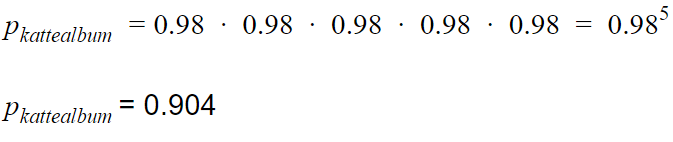
Najs! Med andre ord sannsynligheten for at et påstått kattealbum faktisk inneholder 5 katter er 90.4%.
Men etter en undersøkelse utført blant kunder av vår kjære bedrift, ble det kartlagt at kunder er villig til aksepterte et kattealbum, så sant minst 80% av bildene er av katter.
Så hva skjer hvis vi letter litt på kravene?
For nå å beregne sannsynligheten for å oppnå et kattealbum, gitt at minst 80 % av bildene må inneholde en katt, må vi ta med i beregningen alle mulige album der dette kravet blir oppfylt:
Her har vi først et album med kun katter, vi har beregnet denne før.
Så for de fem neste albumene må vi bruke følgende beregning:
Dermed vil sannsynligheten for å få til et kattealbum med 5 bilder, gitt kravet om at minst 80% av bildene skal være katt, summen av sannsynligheten for hvert mulige album:
Aiit, aiit! Med å lette på kravene har vi nå en sannsynlighet for å lage et kattealbum på 99.6% 
Meeen er det egentlig så enkelt? 
For å svare på dette må vi ta en titt på de fire forskjellige albumene vi kan oppnå:
Vi har ekte kattealbum, ekte gratis album, falske kattealbum og falske gratis album.
Hvilken av disse kan vi argumentere rundt takket være beregningene vi gjorde over?
Vi kan beskrive ekte kattealbum, sannsynligheten for å oppnå et kattealbum som faktisk er et kattealbum er 99.6%.
Vi kan også beskrive et falsk gratis album, dette er et kattealbum som faktisk er et kattealbum, men som ble feilaktig markert som et gratis album. Dette får vi ved å gjøre følgende beregning:
(1 - 0.996) * 100 = 0.4%.
Men hva med ekte gratis album og falske kattealbum?
Vi vet at ledelsen er spesielt opptatt av rykte og omdømme, og det er derfor svært viktig at kunder ikke betaler for noe de ikke får. Det blir det mye klager av i følge kundeservice.
Da må vi finne sannsynligheten for å generere et falskt kattealbum.
Sannsynligheten for å feilaktig klassifisere et bilde er: 1 - 0.98 = 0.02.
Dermed blir sannsynligheten for å markere et album helt uten kattebilder, som et kattealbum:
Not too shabby! Det virker da veldig bra at det skjer så sjeldent.
Men!

Vi letta jo på kravene til produksjonen av kattealbum, dette for å redusere sannsynligheten for falske gratis album.
Kravet ble endra til at minst 80% av bildene må være av katt.
Da må vi i tillegg til beregningen ovenfor legge til sannsynligheten for å lage et falsk kattealbum der 4 av 5 bilder er feilaktig detektert som katt, mens 1 bilde er riktig detektert som ikke katt.
Da får vi følgende:
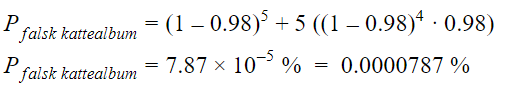
Så, når vi tidligere elegant reduserte sannsynligheten for å gi bort kattealbum gratis med ca 10 prosentpoeng, så økte vi sannsynligheten for å selge falske kattealbum med 0.0000784 prosentpoeng.
Det ser jo ikke så gæli ut?
Men hva hvis vi omformulerer utsagnet litt?
Vi kan også beskrive endringene ved at vi gir bort 24 ganger færre kattealbum gratis enn før samtidig som vi selger 246 ganger flere gratis album feilaktig som kattealbum.
Det som er interessant her er at ved å redusere en feil, så øker man den andre og motsatt.
Spørsmålet blir dermed hvilken feil vil interessentene prioritere å redusere?
Midlertidig konklusjon
Vi ser at selv om andelen feil-solgte album øker med hele 246 ganger, er sannsynligheten for å faktisk feilaktig selge et gratis album ekstremt lav.
Her må man avveie hvilken type feil det er som er mest kritisk for interessentene og justere parametrene i problemstillingen deretter.
Men wait, skulle ikke vi snakke om “kumulativ binomisk sannsynlighet”?
Joda! Det kom med neste steg i utviklingen av problemstillingen.
Hva gjør vi hvis vi ønsker å enkelt kunne eksperimentere med de ulike parametrene vi har brukt så langt for å raskt finne frem til den mest gunstige parametersamensetningen for å dekke interessentenes krav?
Hvordan vil regnestykket se ut hvis kundene kjøper album med 7, 12 eller 32 bilder?
Hva vil skje hvis vi øker eller senker kravet til andel katter i hvert album? Og hvordan påvirker dette feilene vi ønsker å unngå?
Kumulativ Binomisk Sannsynlighet
For å finne en generell enkel måte å gjennomføre disse beregningene for alle mulige kombinasjoner av parameterne begynte jeg å lete i statistikk-boka jeg brukte på NTNU.
Og ser man det, det var noen smartinger som allerede hadde funnet løsningen på mitt problem!
Det jeg hadde febrilsk prøv å løse var et såkalt binomisk eksperiment!
Et binomisk eksperiment har følgende karakteristikker:
- Flere forsøk
- Hvert forsøk har 2 mulige resultat
- Sannsynligheten for hvert forsøk er lik, med andre ord konstant
- Alle forsøk er uavhengige
Formelen for binomisk sannsynlighet er som følger:
![]()
p = sannsynlighet for positivt resultat i hvert forsøk (0.98 i vårt tilfelle)
n = antall forsøk, i vårt tilfelle størrelsen på albumet
x = antall positive tilfeller, med andre ord antallet kattebilder i albumet
Hvis vi nå bruker denne formellen til å løse problemene vi allere har løst ser vi at vi får:
Gitt et album med 5 bilder, der alle 5 skal være av katter:
![]()
Gitt et album der nøyaktig 80% er av katter, da får vi:
![]()
Og sannsynligheten for at albumet minst inneholder 80% katter:
0.904 + 0.0922 = 0.996 = 99.6%
Vi ser at dette gir oss de samme resultatene som vi kom frem til tidligere.
Snipp Snapp Snute
For å gjøre vår lille fortelling komplett tar vi å slår i sammen formelene nevnt ovenfor til formelen for kumulativ binomisk sannsynlighet:
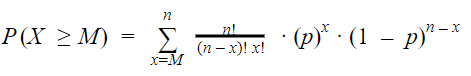
p = sannsynlighet for positivt resultat i hvert forsøk (0.98 i vårt tilfelle)
n = antall forsøk, i vårt tilfelle størrelsen på albumet
M = minimum antall positive tilfeller, med andre ord antallet kattebilder i albumet
Puh… Det ble en munnfull!
Er det noen andre som har lignende historier der tidligere antatt unyttige elementer fra skolegangen plutselig viser seg å være svært så nyttige?
TO BE CONTINED…
Der finnes et steg til i denne problemstillingen som jeg har sett på. Hva hvis man vet distribusjonen for kundenes kjøpsmønster? Med andre ord hvor stor andel av solgte album har en gitt størrelse?
Hvordan kan denne kunnskapen brukes til å justere parametrene i vår problemstilling for å redusere antallet tilfeller av feilaktig solgte album?





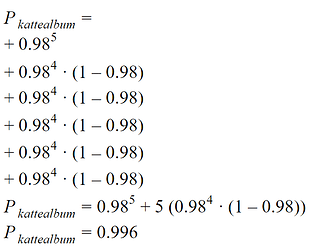

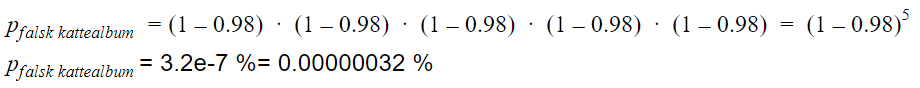
 og de kattebildene var velvalgte, skjønner hvorfor de selger så bra
og de kattebildene var velvalgte, skjønner hvorfor de selger så bra 