Dette er en oppfølgings post til en tidligere introduksjon av algoritmen Minimax her på forumet. Hvis du ikke er kjent med Minimax fra før kan jeg anbefale at du starter der.
Som nevnt i slutten av posten har Minimax en svakhet i at tidskompleksiteten gror eksponentielt med dybden i søketreet til problemet, O(antall-mulige-trekk^dybde). Det finnes heldigvis utvidelser av algoritmen som gjør den langt mer effektiv. Jeg tenkte vi skulle se på en av disse, nemlig Alpha-Beta pruning. Som navnet hinter til, er formålet med denne utvidelsen å fjerne noen av forgreningene i søke-treet.
Alpha-beta pruning varianten av Minimax introduserer to variabler, Alpha og Beta:
- Alpha: Den beste garanterte verdien (høyeste) for Max som er funnet ved et gitt tidspunkt i søke-prosessen.
- Beta: Den beste garanterte verdien (laveste) for Min som er funnet ved et gitt tidspunkt i søke-prosessen.
På samme måte som Minimax, utføres også her en type rekursiv dybde-først søk. Den nye idéen er å huske på hva det beste mulige utfallet fra et gitt valg for Min og Max underveis i søket er, for så å bruke denne kunnskapen til å avslutte søk langs en gren så fort vi kan vite at et gitt valget aldri kommer til å bli gjort.
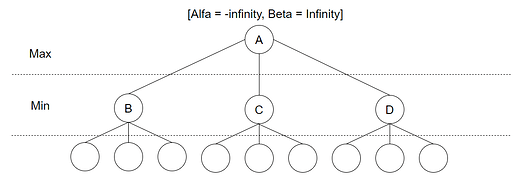
La oss start med å re-introdusere det enkle spillet fra Minimax posten:
- Det er to spillere, Min og Max.
- Spillet består av en runde, hvor hver spiller gjør ett trekk.
- I hvert trekk har spilleren tre muligheter.
- Max starter og ønsker maksimal verdi.
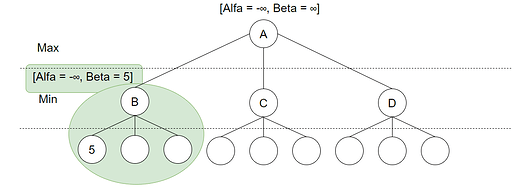
Ved start av spillet er Alpha satt til -uendelig, mens Beta er satt til +uendelig. Hver node starter med å arve Alpha og Beta verdi fra sin forelder-node. Søket starter så med et dybde-først søk, la oss si mot B:
Når søket når en løv-node kalles evalueringsfunksjonen, og her finner vi 5. Siden dette er et valg som skal utføres av Min vil Beta bli satt til den minste verdien av evalueringsfunksjonens resultat og nå-værende beta-verdi (+uendelig). Beta blir da satt til 5. Deretter kalles evalueringsfunksjonen på den neste løv-noden:
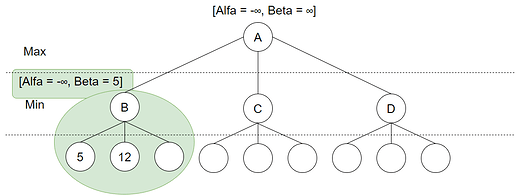
Resultatet sammenlignes med Beta som nå er 5. Siden 5 er mindre enn 12, og dette valget skal utføres av Min skjer det ingen endring, og siste løv-node knyttet til B utforskes:
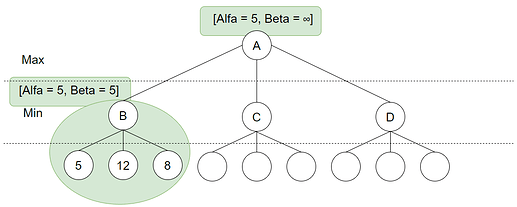
Her gir evalueringsfunksjonen 8, dette er heller ikke mindre enn 5 og Beta endres derfor ikke. Men vi har nå utforsket alle av B sine løv-noder og vi kan nå konkludere med at Max kan garantere seg 5 ved å ta dette valget, vi setter derfor Alpha til å være lik 5. Siden Max kan velge å gå til B (høyre), kan vi flytte denne Alpha-verdien tilbake til rot-noden, mens Beta her forblir -uendelig, siden Min ikke kan garantere at Max velger å gå mot B. Videre utføres dybde-søk mot C og vi utforsker første løv-node:
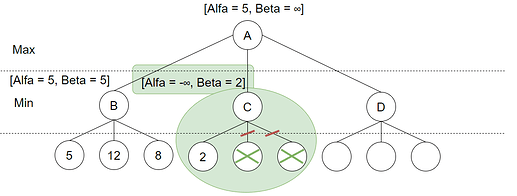
Og her skjer det ting! Evalueringsfunksjonen har returnert 2. Men vi vet at Max kan oppnå 5 ved å gå til B, og siden dette valget skal utføres av Min og vi vet at Min ønsker å minimere verdien kan vi konkludere med at Max aldri vil gjøre dette valget. Vi trenger heller ikke fortsette å utforske de andre løv-nodene knytte til C. Vi har ikke funnet en ny og bedre verdi for Alpha, og vi kan heller ikke garantere Min at C blir valgt så Alpha og Beta forblir uforandret for rot-noden. Vi utfører så dybde-først søk mot D:
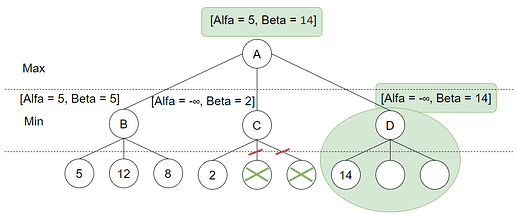
Første løv-node evalueres og verdien 14 returneres. Denne er lavere en uendelig, så Beta oppdateres for D. På dette tidspunktet kan vi også si at Min kan garantert få maks 14, derfor oppdateres også rot nodens Beta. Søket forsetter så ved neste løv-node:
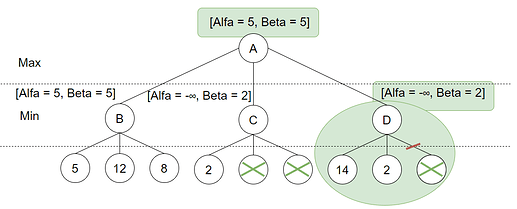
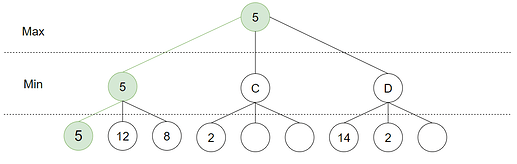
Her er vi nok en gang heldige og finner 2. Det følger da av samme logikk som for node C at Max aldri vil velge D og vi kan “prune” vekk den siste løv-noden. På dette tidspunktet er også alle noder som kan ha en effekt på det endelige resultatet undersøkt. Vi vet nå at Max vil gå mot B og vi kan derfor garantere Min og ikke få høyere enn 5, dermed settes Beta lik 5 for rot-noden. Til slutt kan vi konkludere med at spillet vil blir utført som følgende:
Ganske kult, ikke sant? En nyttig observasjon er at effektiviteten til algoritmen er avhengig av rekkefølgen løv-nodene blir sjekket i. Det kan derfor være nyttig å lage en funksjon som bestemmer dette. For sjakk kan det være å sjekke trekk som resulterer i at en brikke blir tatt, deretter trekk som putter brikker i posisjon hvor de kan bli tatt osv. I posten om Minimax kom jeg med en litt unyansert uttalelse, hvor jeg sa at tidskompleksiteten kan reduseres til O(antall-mulige-trekk^(dybde/2)) med Alfa-Beta-pruning. Det er i og for seg sant, men gjelder kun hvis man finner en funksjon som gjør utforsknings-rekkefølgen perfekt. Men selv om rekkefølgen velges tilfeldig, reduseres tidskompleksiteten til O(antall-mulige-trekk^(3*dybde/4)).
Alpha-beta-pruning er altså en spesialiseringsvariant av Minimax. Det finnes en rekke lignende algoritmer, hvor man utvider bruksområdet til stokastiske og delvis observerbare domener. Jeg gleder meg til å lære om dem en dag 

 takk!
takk!