Minimax er en søkealgoritme som benyttes i “adversarial search” problemer som også kalles “spill”. Algoritmen og varianter av algoritmen kan benyttes i en rekke type spill, og vi skal nå utforske den i kontekst av spill som oppfyller følgende krav:
- Spillet er deterministisk og zero-sum.
- Spillerne har perfekt informasjon.
- Spillerne alternerer om hvem som utfører neste handling.
- Det er kun 2-spillere.
- Begge spiller optimalt.
Et eksempel på slike spill kan være tre-på-rad, dam eller sjakk. Spillene kan sees på som søke-problemer da hvert trekk resulterer i en ny state i spillet, disse gir igjen opphav til nye mulige trekk, basert på foregående trekk osv. Dette kan enkelt modelleres som et søketre.
Videre definerer vi 2 spillere, Max og Min. Max ønsker å maksimere verdien av en state mens Min ønsker å minimere den.
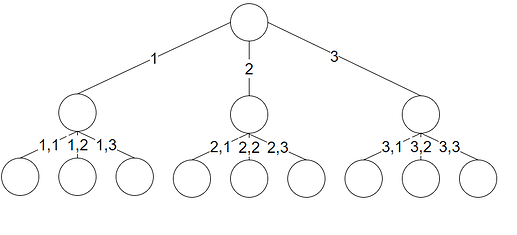
For spill som tre-på-rad vil spiller 1 (Max) først ha 9 mulige valg, ut ifra valget vil spiller 2 (Min) ha 8 valg osv. Dette kan modelleres med et komplett tre som vil ha under 9 fakultet (362,880) terminalnoder (mange av disse like), og vi kan ved å analysere disse konkludere med at et hvert spill skal resultere i uavgjort så lenge begge spiller optimale trekk.
For et spill som sjakk består derimot det komplette treet av 10^40 forskjellige noder. Det er med andre ord helt utenkelig å konstruere det komplette treet. I slike spill blir man nødt til å bestemme seg for en gitt dybde man ønsker å søke til, for så å benytte en heuristisk evalueringsfunksjon for å definere verdien i daværende tilstand av spillet.
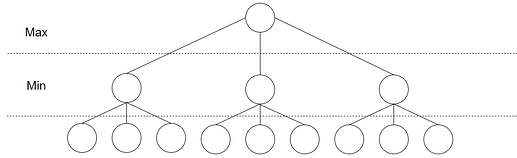
Så, med denne bakgrunnskunnskapen kan vi ta en titt på hvordan Minimax fungerer. Den starter med å gjøre en form for rekursiv dybde-først søk. For å illustrere hvordan algoritmen jobber la oss definere et enkelt spill:
- Det er to spillere, Min og Max.
- Spillet består av en runde, hvor hver spiller gjør ett trekk.
- I hvert trekk har spilleren tre muligheter.
- Max starter og ønsker maksimal verdi.
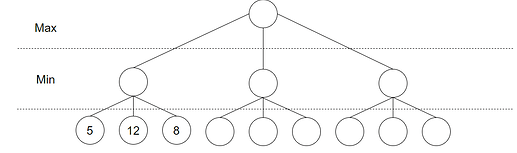
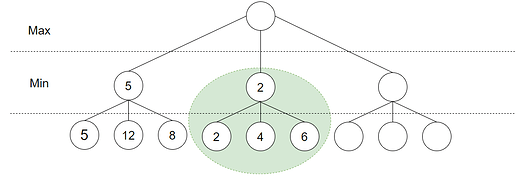
Algoritmen starter med å utforske nodene til venstre. Når den treffer en løv-node bruker den en evalueringsfunksjon for å finne verdien i staten denne noden representerer. Etter å ha funnet de tre løv-nodene til venstre vil det se lik ut:
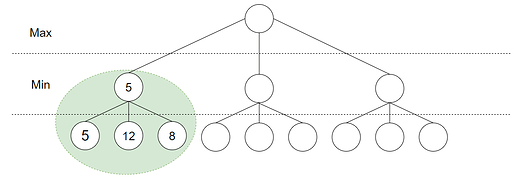
Siden disse er knyttet til en Min node, vil den minste verdien bli valgt:
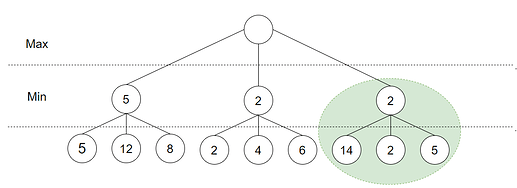
Algorimen går tilbake til toppen, her ser vi at flere av barne-nodene enda ikke er utforsket og søket forsetter i det miderste sub-treet. Evalueringsfunksjonen blir kalt på løv-nodene og den laveste blant dem valgt:
Vi returnerer til rot-noden før høyresiden utforskes:
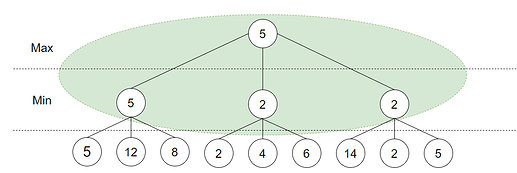
Da har alle barne-nodene til rot-noden blitt utforsket og det er Max sin tur. Max ønsker å maksimere verdien og velger 5:
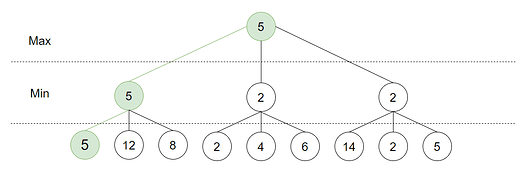
.Hele treet er nå undersøkt og minimax verdien 5 er funnet. Dette er den høyeste verdien Max kan oppnå da han vet Min spiller optimalt og ønsker å minimere denne verdien. Spillet vil bli utført som følgende:
Så, kan en såpass enkel algoritme brukes for å løse komplekse problemer? Hvis vi går til dybde N og på hver node har X mulige trekk vil tidskompleksiteten være lik O(X^N). Med andre ord vil algoritmen være for ineffektiv til de aller fleste sanntidsapplikasjoner hvor beregningstid er en begrensende faktor. Men algoritmen danner en basis for analyse av en rekke spill og ikke minst er den et utgangspunkt for flere mer praktisk-anvendbare algoritmer. En av disse er Minimax med Alpha-Beta-pruning. Ved å gjøre et par smarte triks, klarer den å halvere N slik at tidskompleksiteten reduseres til O(X^(N/2)).
Fortsettelse følger…